limour/limour-blog.github.io

title: 【迁移】使用MICE包对数据缺失值进行插补 urlname: shi-yong-MICE-bao-dui-shu-ju-que-shi-zhi-jin-hang-cha-bu date: 2022-09-10 18:08:59 index_img: https://api.limour.top/randomImg?d=2022-09-10 18:08:59

tags: [MICE, R]

在分析数据集时，常常会碰到一些缺失值，如果缺失值的数量相对总体来说非常小，那么直接删除缺失值就是一种可行的方法。但某些情况下，直接删除缺失值可能会损失一些有用信息，此时就需要寻找方法来补全缺失值。

安装包

conda create -n mice conda-forge::r-tidyverse conda-forge::r-irkernel conda-forge::r-mice conda-forge::r-vim
conda run -n mice Rscript -e "IRkernel::installspec(name='mice', displayname='mice')"

导入数据

library(tidyverse)

airquality %>% head()
colnames(airquality) <- str_replace_all(colnames(airquality), pattern = '\\(| |-', replacement = '_')
colnames(airquality) <- str_replace_all(colnames(airquality), pattern = '\\)', replacement = '')
airquality %>% summarise_all(~ round(sum(is.na(.)) / length(.), 3))

airquality <- airquality %>% 
    mutate(Month = factor(Month)) %>% 
    mutate(Day = factor(Day))

查看数据质量

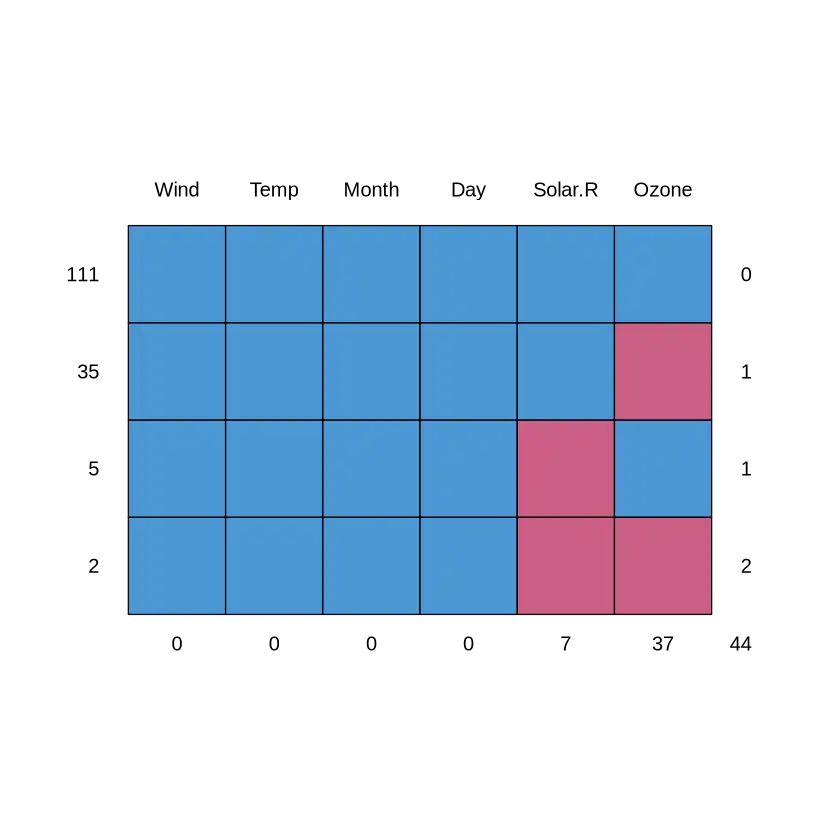
mice::md.pattern(airquality)

左边第一列，为样本数
右边第一列，为累积缺失值个数，0为没有缺失。
第一行可以理解为，有111条记录，所有列都有值，没有缺失值。

第二行可以理解为，有35条记录，Ozone列有缺失值。

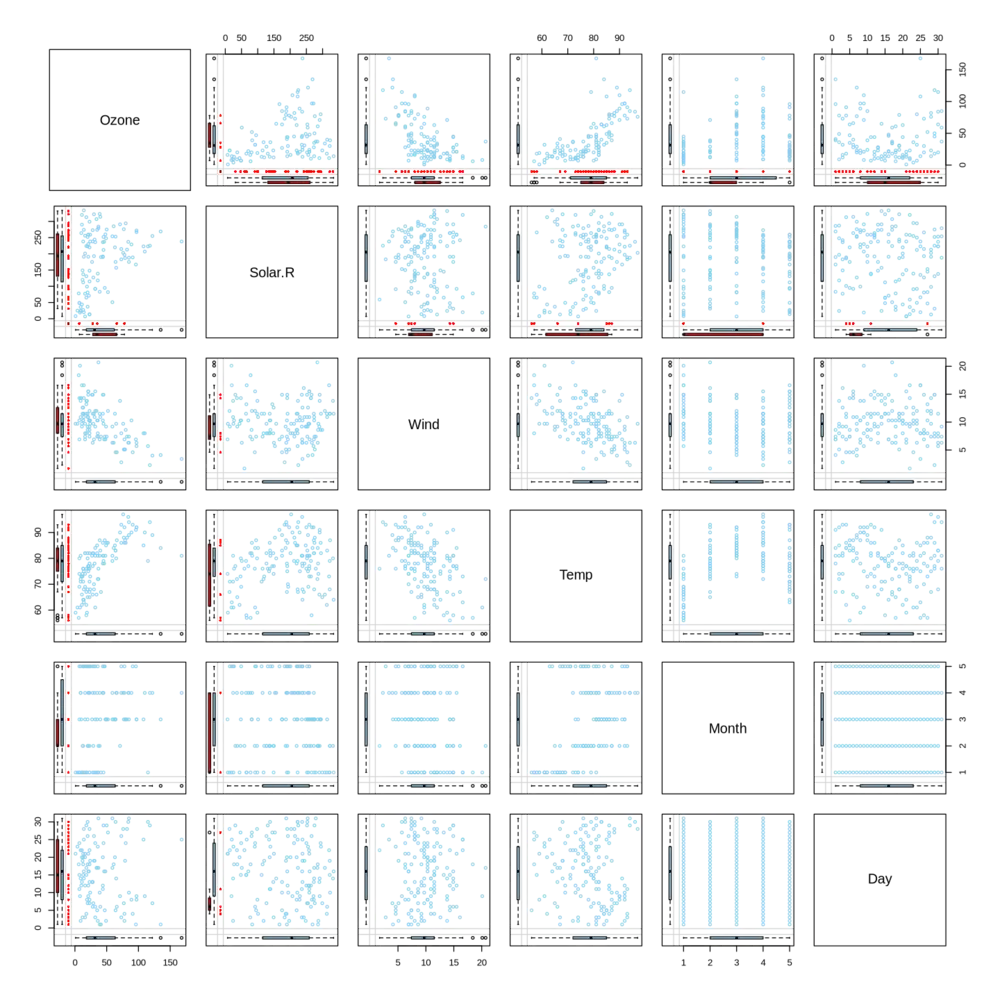
options(repr.plot.width = 12, repr.plot.height = 12)
VIM::marginmatrix(airquality)

当同一侧红蓝箱线图较为接近时可认为其对应考察的另一侧变量缺失情况比较贴近完全随机缺失，这种情况下可以放心大胆地进行之后的插补，否则就不能冒然进行插补。

options(repr.plot.width = 6, repr.plot.height = 6)
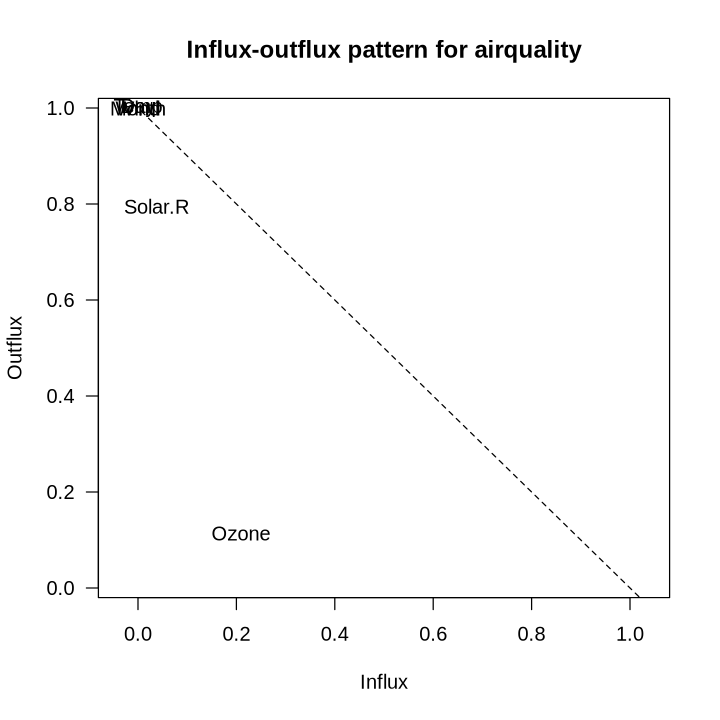
mice::fluxplot(airquality)

通量图可用于发现潜在的预测因子、更容易被预测的变量以及干扰插补模型的变量。一般来说，离对角线较近的变量通常比距离较远的变量关联性更好（关联性好的预测性更好），位于较低区域（尤其是左下角附近）且对后续分析不感兴趣的变量最好在插补之前从数据中删除。

mice包介绍

mice包实现了，多变量缺失数据填补的方法，基于多元回归模型来预测，每个不完整变量由单独的模型估算，进行多重混合评估。mice包算法可以实现对于连续型，二进制，无序分类和有序分类数据的进行混合。此外，mice包可以处理连续的两级数据，并通过被动插补来保持插补之间的一致性，通过各种统计诊断图，保证插补数据的质量，该包论文在统计软件领域顶刊JSS上。(from 粉丝日志)

对于缺失值数据的处理，用3个步骤来进行定义。

填充：mice()函数，从一个包含缺失数据的数据框开始，然后返回一个包含多个完整数据集的对象，每个完整数据集都是通过对原始数据框中的缺失数据进行插而生成的。
分析：with()函数，可依次对每个完整数据集应用统计模型，分析填充的结果。

优化：pool()函数，将这些单独的分析结果整合为一组结果，最终模型的标准误和p值，都将准确地反映出由于缺失值和多重插补而产生的不确定性。

van Buuren, S., & Groothuis-Oudshoorn, K. (2011). mice: Multivariate Imputation by Chained Equations in R. Journal of Statistical Software, 45(3), 1–67. https://doi.org/10.18637/jss.v045.i03

进行迭代插补

# 这里认为日期对于其他变量无相关关系，因此令变量Month与变量Day不参与对其他变量的拟合插补过程
irrelevant_variable <- c('Month', 'Day')
predictorMatrix <- mice::quickpred(airquality, mincor = 0.1, minpuc = 0, include="", exclude = irrelevant_variable, method = "spearman")
# mincor：向量或矩阵，指定最小的阈值，利用被预测和预测变量的相关系数绝对值大于等于该值的的预测变量进行插补，默认为0.1；
# minpuc：指定可用个案数的最小比例；
# include：指定必须包含的变量；exclude：指定排除的变量；
# method指定相关的类型，有pearson、kendall和spearman。

predictorMatrix %>% as.data.frame  %>% sapply(sum)
predictorMatrix  %>% t %>% as.data.frame  %>% sapply(sum)
predictorMatrix

#初始化插补模型,这里最大迭代次数选0是为了取得未开始插补的朴素模型参数
init <-  mice::mice(airquality, predictorMatrix = predictorMatrix, maxit=0, seed=1337)
init$loggedEvents  # 看是否有共线性等事件

# 修改每一个变量对应的插补方式
init$method[c('Ozone', 'Solar.R')] = 'cart' # 决策树回归
# meth：指定数据中每一列的输入方法。
# 1）数值型数据适用 pmm；
# 2）二分类数据适用 logreg；
# 3）无序多类别数据适用 ployreg；
# 4）有序多分类变量适用 polr。
# 默认方法为 pmm 
# Can be either a single string, or a vector of strings with length length(blocks), specifying the imputation method to be used for each column in data.

#利用修改后的参数组合来进行拟合插补
imputed <- mice(airquality, method = init$method, predictorMatrix = init$predictorMatrix, m=5, seed=1337, maxit=500)
# m: 生成插补矩阵的个数，mice最开始基于gibbs采样从原始数据出发为每个缺失值生成初始值以供之后迭代使用，而m则控制具体要生成的完整初始数据框个数，在整个插补过程最后需要利用这m个矩阵融合出最终的插补结果，若m=1，则唯一的矩阵就是插补的结果；

options(repr.plot.width = 6, repr.plot.height = 6)
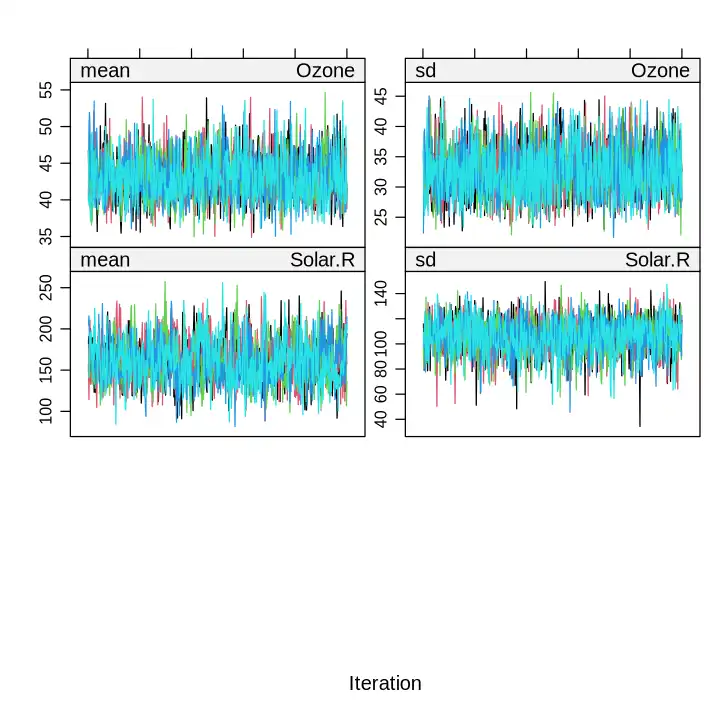
plot(imputed)
# 结果显示的是插补值得均值（左）和标准差（右），
# 如果线迹充分混合且没有趋势，表明算法收敛良好，一般默认的5次迭代就可以达到很好的效果。

选择合适的插补（看图）

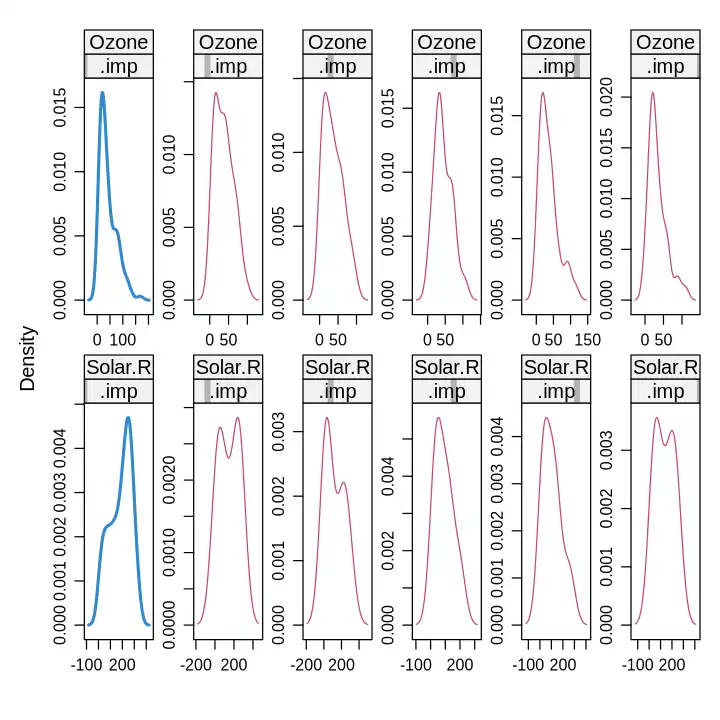
mice::densityplot(imputed, ~ Ozone + Solar.R | .imp)
# 蓝色为原始数据的分布，第一幅红色图为一重插补，以此类推，选择最符合的

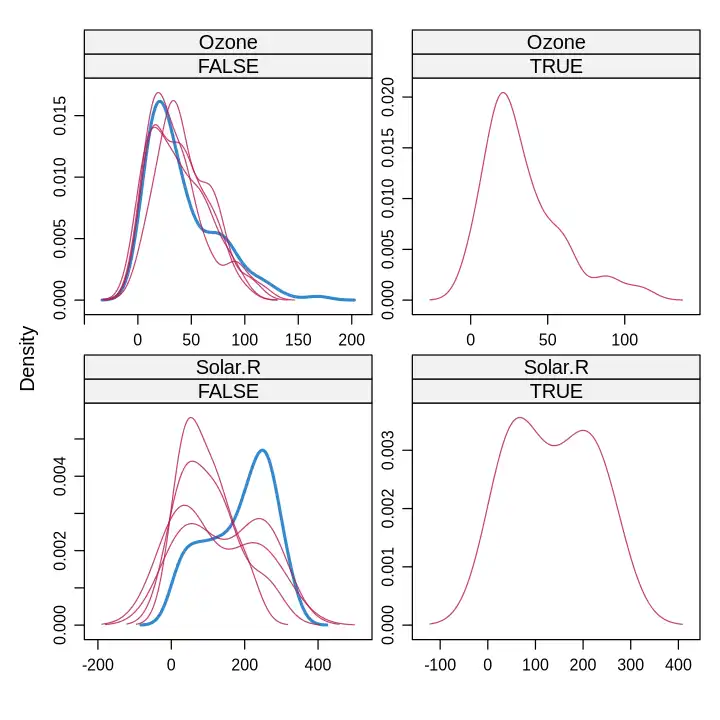
mice::densityplot(imputed, ~ Ozone + Solar.R | .imp == 5)
# 具体查看某一重插补，蓝色为原始数据的分布，右侧为选择的插补。

导出插补后的数据

f_mice_complete <- function(l_data, l_imputed, l_colname, action){
    l_data[rownames(l_imputed$imp[[l_colname]]), l_colname] <- l_imputed$imp[[l_colname]][action]
    return(l_data)
}
Data <- imputed$data
Data <- f_mice_complete(Data, imputed, 'Ozone', 4)
# 根据检验统计量，我们选择以第4次的结果做为Ozoned的填充，获得填充后的数据集。
Data <- f_mice_complete(Data, imputed, 'Solar.R', 2)
# 根据检验统计量，我们选择以第2次的结果做为Solar.R的填充，获得填充后的数据集。

插补的不确定性

fit1 <- with(imputed, stats::lm(formula('Ozone ~ Solar.R + Wind + Temp')))
fit2 <- with(imputed, stats::lm(formula('Solar.R ~ Ozone + Wind + Temp')))
mice::pool.r.squared(fit1)
mice::pool.r.squared(fit2)
# est, 合并的R^2，估计值
# fmi，缺少信息的部分，越小越好

插补数据集分析

fit <- with(imputed, ...) # 对插补后的每个数据集都进行模型拟合
# ... 为用来设定应用于m个插补数据集的统计分析方法，比如 lasso
# 理论上，只要函数符合R中的coeff方法的准则规范，用其进行多次插补后的结果都可以用pool函数进行汇总，
# 而且pool.scalar函数可以“手动”汇总m个重复完整数据的单变量分析估计值。

est <- pool(fit) # 汇总分析结果
# 结果中几个参数解释如下：
# m：插补次数；ubar：插补组内方差的均值；
# b：插补间方差；
# t：合并估计的总方差（笔者觉得应该是标准误的平方；
# dfcom：插补数据集的自由度；
# df：假设检验的残余自由度；
# riv：因缺失导致的方差相对增加；
# lamba：由于缺失而导致的总方差的比例；
# fmi：因缺失导致的信息（系数）丢失比例。

# 参考：https://mp.weixin.qq.com/mp/appmsgalbum?__biz=MzIzNjk2NDg4NA==&action=getalbum&album_id=2677603372061081601&subscene=159&subscene=190

插补的环境

date()
for (packagename in (.packages())){
    print(packageDescription(packagename))
}

2022-09-10-【迁移】使用MICE包对数据缺失值进行插补.md 8.6 KB Bezpośredni odnośnik Historia Czysty